EM/GMM¶
Gaussian Mixture Models: Estimate Mixtures of \(K\) Gaussians
- pick sample from gaussian \(k\) with prob. \(\pi_k\)
- generative distribution \(p(\mathbf{x}) = \sum_{k=1}^K \pi_k N(\mathbf{x} | \mathbf{\mu}_k, \mathbf{\Sigma}_k)\)
- where \(N\) is the gaussian distibution
- a mixture distribution with mixture coefficients \(\mathbf{\pi}\)
- for iid sample \(\mathbf{X}\) and parameters \(\theta = \{\mathbf{\pi}, \mathbf{\mu}, \mathbf{\Sigma}\}\), we have:
\[\begin{split}p(\mathbf{X} | \mathbf{\pi}, \mathbf{\mu}, \mathbf{\Sigma}) & = \prod_{n=1}^N p(\mathbf{x_n} | \mathbf{\pi}, \mathbf{\mu}, \mathbf{\Sigma}) \\
& = \prod_{n=1}^N \sum_{k=1}^K \pi_k N(\mathbf{x} | \mathbf{\mu}_k, \mathbf{\Sigma}_k)\end{split}\]
What is \(\theta\)?
Log-Likelihood¶
\[\begin{split}L(\pi, \mu, \Sigma) & = \ln p(\mathbf{X} | \mathbf{\pi}, \mathbf{\mu}, \mathbf{\Sigma}) \\
& = \ln (\prod_{n=1}^N \sum_{k=1}^K \pi_k N(\mathbf{x} | \mathbf{\mu}_k, \mathbf{\Sigma}_k)) \\
& = \sum_{n=1}^N \ln (\sum_{k=1}^K \pi_k N(\mathbf{x} | \mathbf{\mu}_k, \mathbf{\Sigma}_k))\end{split}\]
This is very hard to solve directly!
Iteratively¶
- which gaussian picked for \(x_i \in X\) is a latent variable \(z_i\) in \(\{0, 1\}^K\) (one of K encoding)
- \(Z\) is vector of \(z_i\)’s
- note that \(p(\mathbf{X} | \mathbf{\pi}, \mathbf{\mu}, \mathbf{\Sigma}) = \sum_Z p(\mathbf{X}, Z | \mathbf{\pi}, \mathbf{\mu}, \mathbf{\Sigma})\)
- complete data is \(\{X, Z\}\)
- incomplete data is just \(X\)
- don’t know \(Z\), but from \(\theta^{old}\) can infer


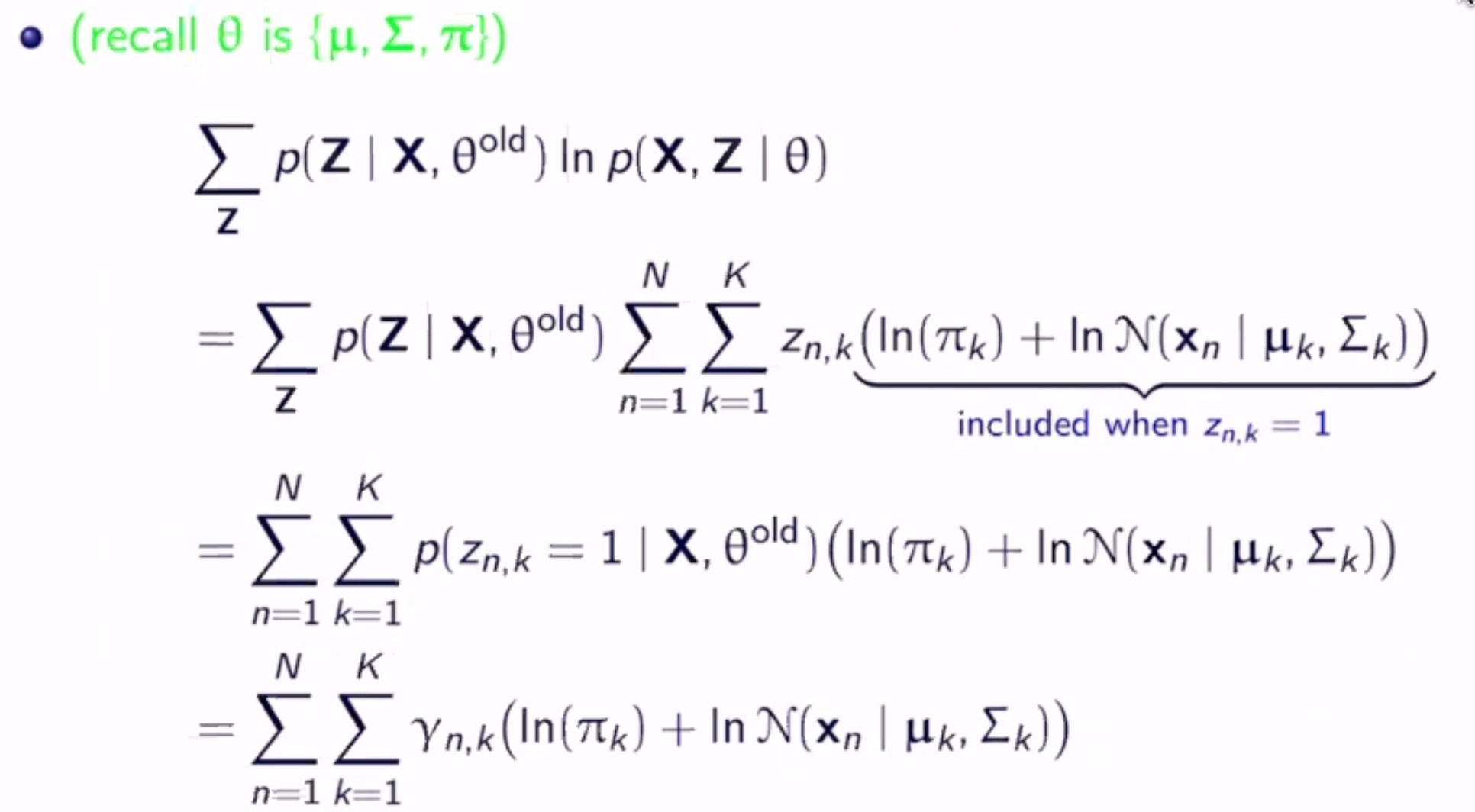
Maximize this to get the new parameters.
