Linear Models¶
If your data is linearly separable, perceptron will find you a separating hyperplane.
But what if my data isn’t linearly separable?
- perceptron will find a hyperplane that makes some errors
- what about a hyperplane that makes a minimal amount of errors?
Minimum Error Hyperplane¶
The error of a linear model \((\mathbf{w}, b)\) for an instance \((\mathbf{x_n}, y_n)\) is:
where \(\mathbf{1}\) is an indicator function that returns 1 on incorrect prediction and 0 on correct (0-1 loss)
Based on this, we can make an objective to minimize the minimum error hyperplane:
This is ERM: empirical risk minimization.
But there are problems:
- the loss fcn is not convex
- not differentiable
Alternatives to 0-1 Loss¶
We need to find an upper-bound to 0-1 loss that is convex, so that minimization is easy. Also, minimizing the upper bound of the objective pushes down the real objective.
Given \(y, a\) (label, activation):
- 0/1: \(l^{(0/1)}(y, a) = 1[ya \leq 0]\)
- hinge: \(l^{(hin)}(y, a) = \max\{0, 1-ya\}\)
- logistic: \(l^{(log)}(y, a) = \frac{1}{\log 2} \log(1 + \exp[-ya])\)
- exponential: \(l^{(exp)}(y, a) = \exp[-ya]\)
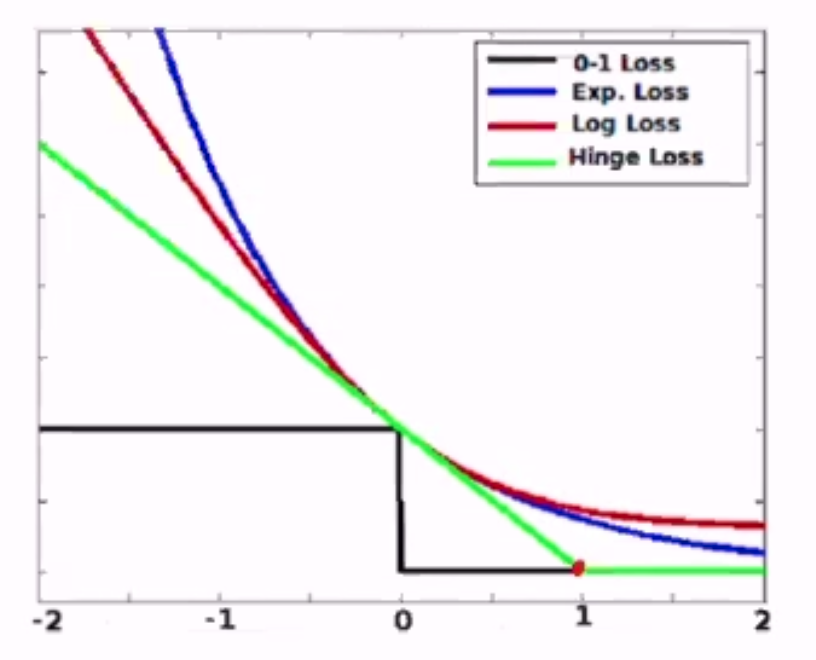
These are all convex functions and can be minimized using SGD - except for hinge loss at point 1.
Sub-gradient Descent¶
How do we minimize a non-differentiable function?
- apply GD anyway, where it exists
- at non-diff points, use a sub-gradient
- sub-gradient of \(f(z)\) at a point \(z'\) is the set of all lines that touch \(f(z)\) at \(z'\) but lie below \(f(z)\)
- at diff points, the sub gradient is the gradient
