Neural Nets¶
Neural nets can be used to approximate nonlinear functions with a hypothesis!
Neural nets are an intuitive extension of perceptron - think of perceptron as a 1-layer neural net.
But in perceptron, the output is just the sign of the linear combination of the inputs - in NN, we use an activation function
Activations should be nonlinear - if they’re linear, it’s redundant
Activations¶
- sign: -1, 0, or 1
- not differentiable
- often used for output layer
- tanh: \(\frac{e^{2x}-1}{e^{2x}+1}\)
- sigmoid: \(\frac{e^x}{1+e^x}\)
- ReLU: \(\max(0, x)\)
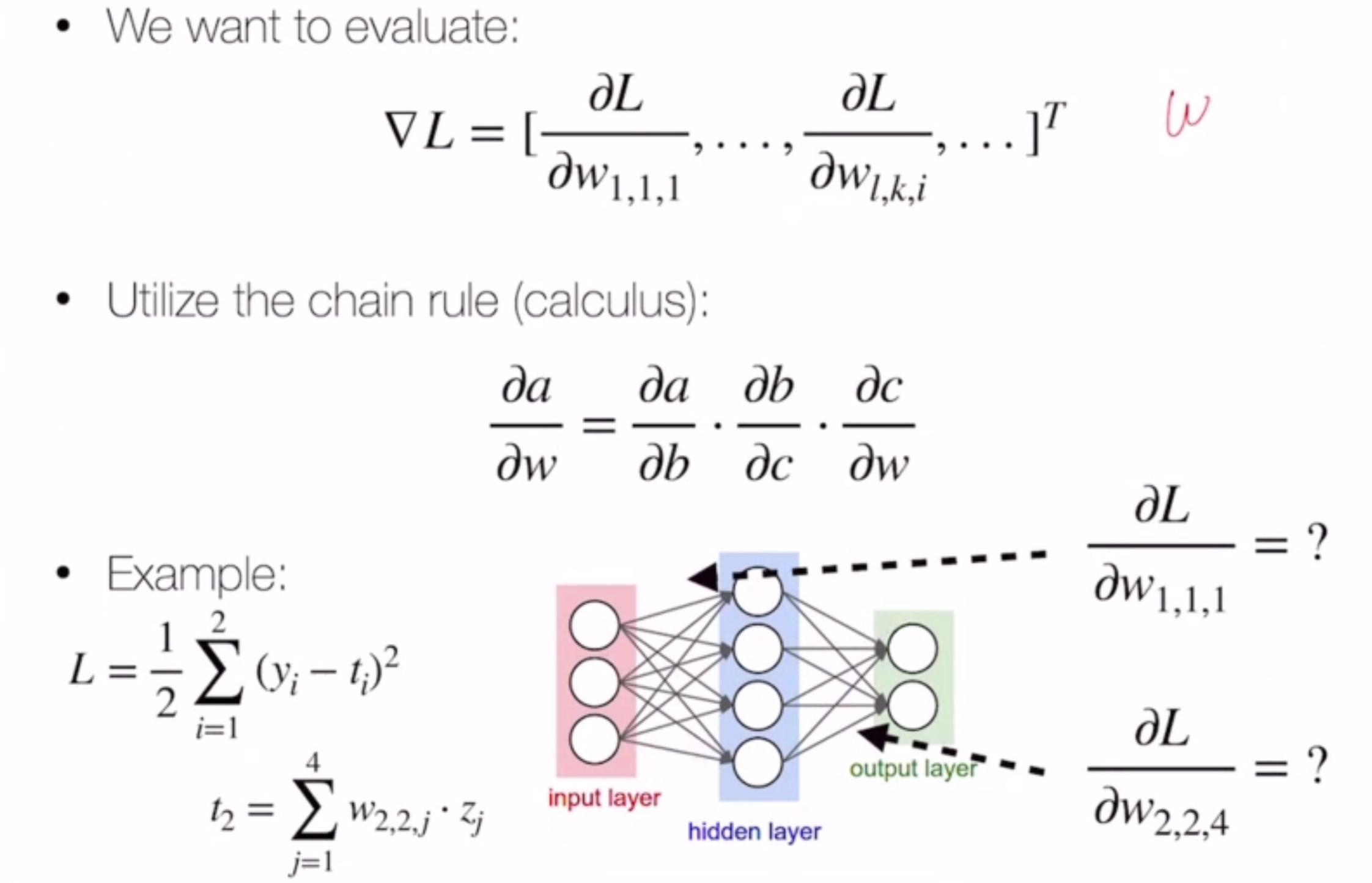
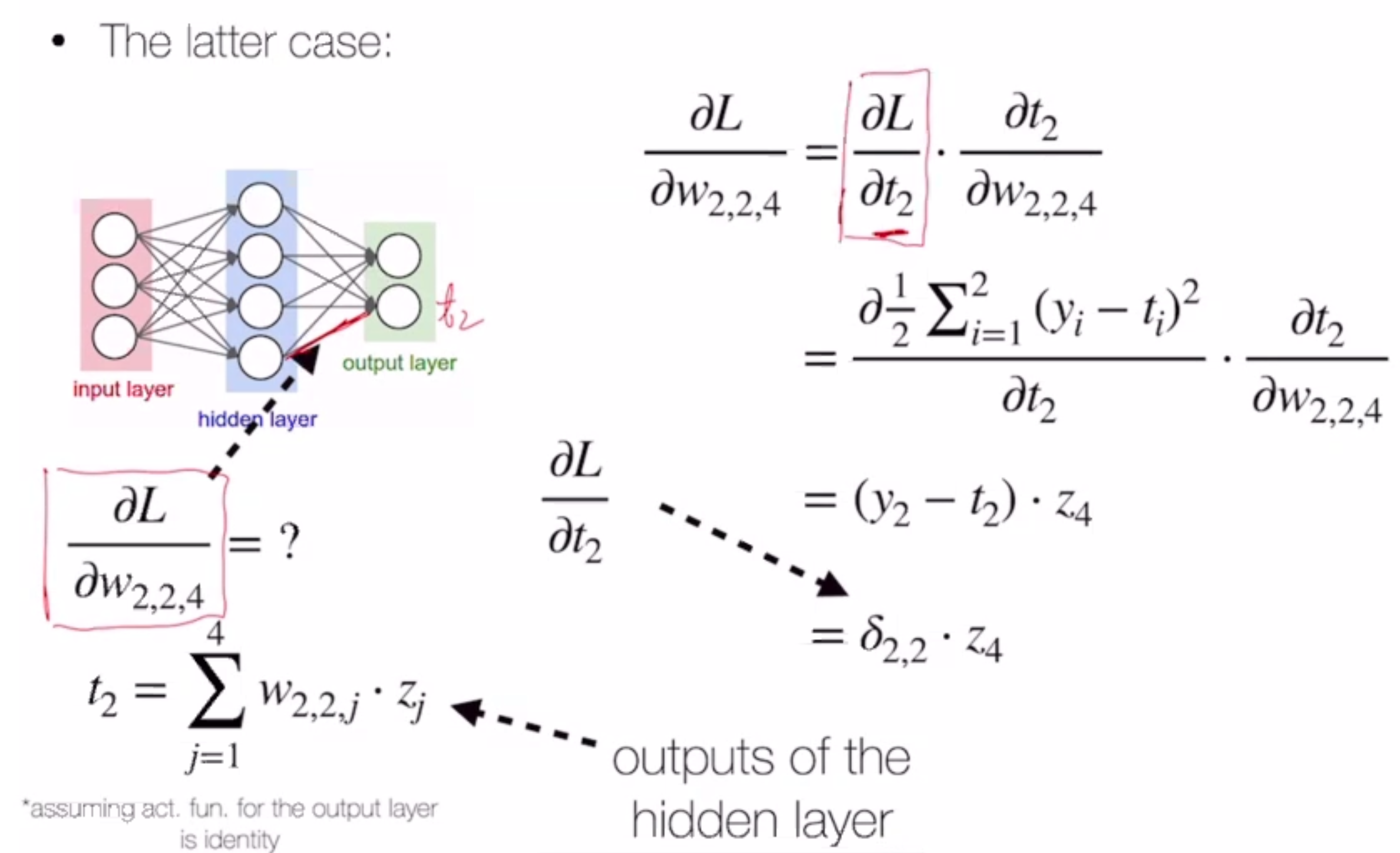
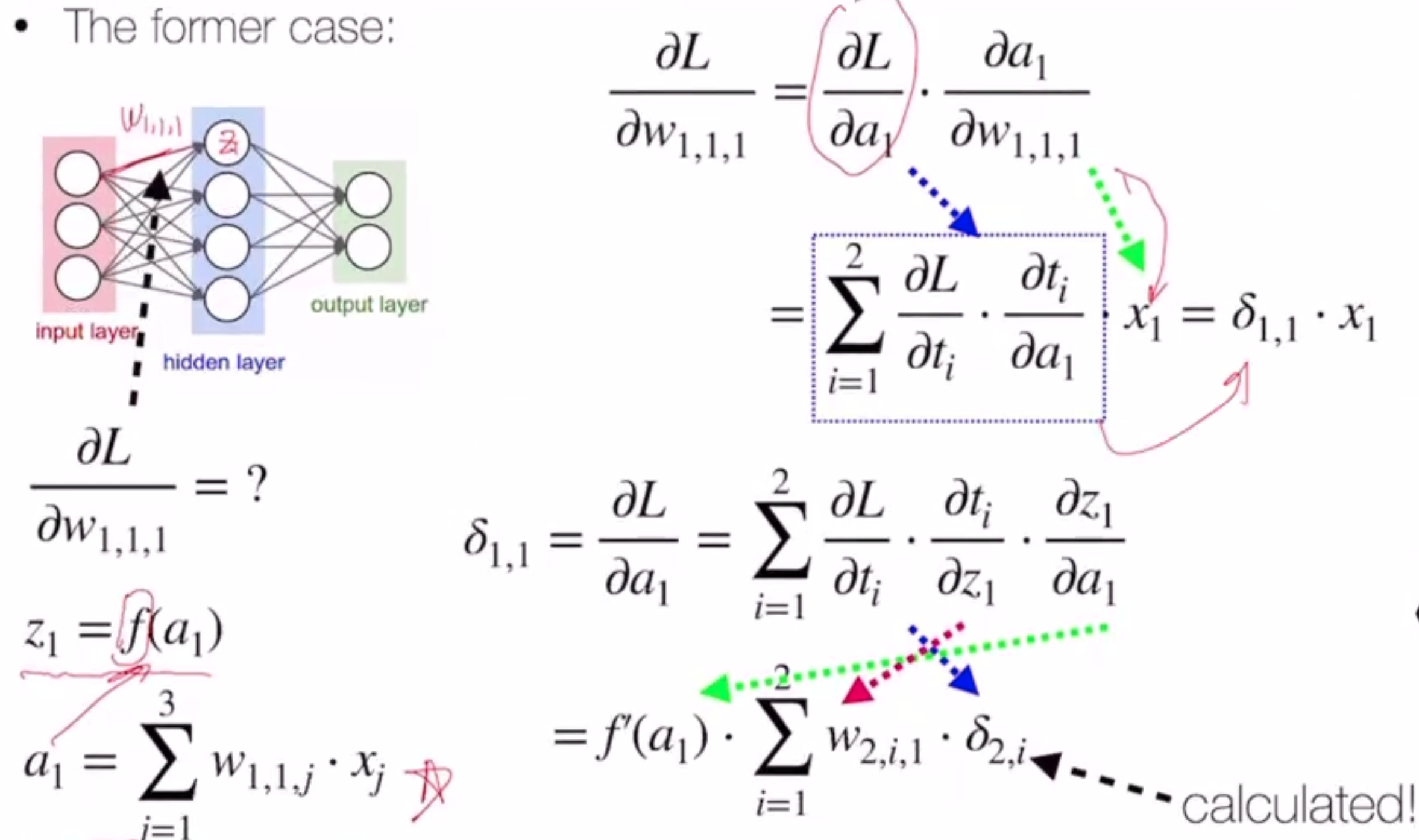
Training¶
Let’s consider the following loss objective on a 2-layer neural net with weights W and v:
we just need to find
We do this using backpropogation.
VAE¶
Whereas normal AE turns images into a latent vector, VAE tries to learn the parameters of a gaussian distribution that the image is a mixture of
where \(c_i\) is a component of the latent vector, \(e_i\) is a random exponential term, and \(m_i\) and \(\sigma_i\) are the gaussian variables.
